Estoy cursando Econometría I por segunda vez. Es una asignatura que siempre me ha parecido algo abstracta y, por eso mismo, la he ido dejando de lado más de lo que debería. Este año empecé motivado, incluso estudié en verano con un profesor particular, pero con el ritmo del curso y las prácticas he vuelto a desconectar… y aquí estoy, a seis días del examen final, escribiendo este artículo para obligarme (por fin) a estudiar de una forma más amena.
Como no quería enfrentarme a la teoría de golpe, he decidido escribir una serie de artículos donde aplique los modelos que hemos visto en clase. La idea es analizar el comportamiento de una acción utilizando modelos de regresión, empezando por el más sencillo: la regresión lineal simple.
La empresa que voy a estudiar es Elecnor, una multinaci española de infraestructuras y energía que cotiza en BME. La conozco desde pequeño porque la empresa de mi padre trabaja con ellos, así que me resulta familiar y cercana. Me parece una buena forma de darle un toque personal al asunto.
Elecnor ha sido uno de los grandes casos de éxito de la bolsa española post-pandemia. Si observamos su gráfico desde los mínimos de marzo de 2020 (entorno a 7,3€) hasta su cotización a día de hoy, diciembre del 2025 (llegando a superar los 30€), vemos una revalorización espectacular superior al 300% en poco más de 5 años.
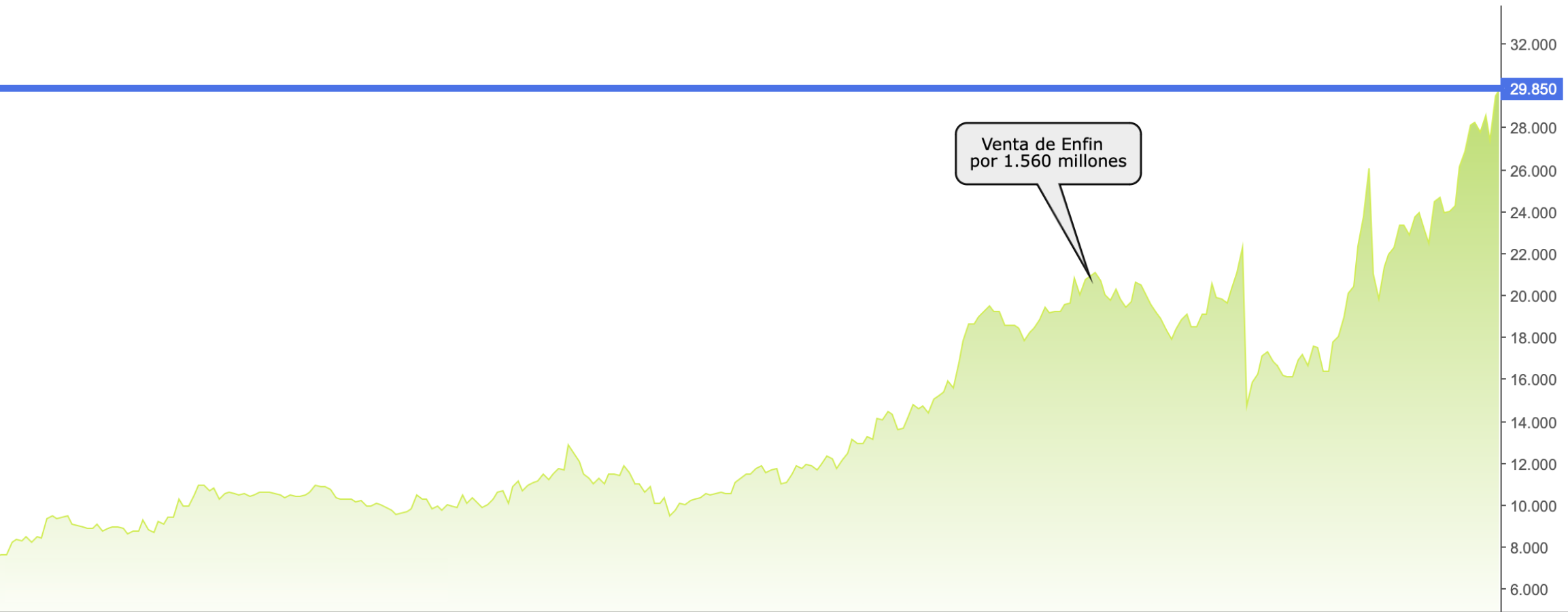
¿A qué se debe este rally? Aunque en este primer análisis nos centraremos en su relación con el Ibex 35, la realidad fundamental detrás de esta subida ha sido el reconocimiento de su valor intrínseco. El mercado tardó en reconocer que la suma de las partes de Elecnor (especialmente su filial de renovables, Enerfin, y su negocio de transmisión, Celeo) valía mucho más que la propia empresa en bolsa.
Esta "ineficiencia" del mercado, que se corrigió finalmente con la venta de Enerfin a Statkraft, es lo que en finanzas buscamos como si fuera el santo grial, el Alpha. Pero, ¿será capaz nuestro modelo de regresión lineal simple de capturar este fenómeno, o necesitaremos herramientas más potentes? Vamos a comprobarlo.
Antes de empezar, dejo algunos datos básicos de la compañía para ponernos en situación (a 4 de diciembre del 2024):
Ticker: ENO
Índice de referencia: Ibex 35
Capitalización bursátil: 2.583 millones €
Precio por acción: 30,5 €
Facturación (2025Q3): 3.150,2 millones €
EBITDA (2025Q3): 185,4 millones €
Ahora sí, ¡vamos con el análisis!
En esta primera parte voy a investigar cómo de sensible es la acción de Elecnor a los movimientos del mercado. La forma estándar de medir esta sensibilidad es calculando su beta, un indicador muy utilizado para evaluar el riesgo sistemático de una acción (es decir, el riesgo que proviene del mercado en su conjunto y que no puedes eliminar diversificando).
Explicado rápido:
\(\beta > 1\) → se mueve más que el mercado (más volátil).
\(\beta < 1\) → acción defensiva, se mueve menos que el mercado.
\(\beta = 0\) → no guarda relación con el mercado.
\(\beta < 0\) → se mueve en sentido contrario al mercado (algo muy poco habitual).
La beta es una pieza importante del modelo financiero CAPM (Capital Asset Pricing Model), que relaciona riesgo y rentabilidad esperada. Aquí no vamos a estimar el CAPM completo, simplemente vamos a usar su idea básica para ver cómo el rendimiento de Elecnor responde a los movimientos del Ibex 35 mediante una regresión lineal simple.
Nota. En este primer análisis estoy utilizando una versión simplificada del CAPM. Comparo la rentabilidad de Elecnor y la del Ibex 35, sin ajustar por la tasa libre de riesgo. En futuros análisis aplicaremos el CAPM tal y como lo plantea la teoría.
¿Qué hipótesis queremos contrastar?
Como queremos saber si Elecnor se mueve (de forma sistemática) con el mercado:
\(H_0: \beta_1 = 0\) → Elecnor no se mueve con el mercado.
\(H_1: \beta_1 ≠ 0\) → Elecnor sí responde a los movimientos del mercado.
Si rechazamos la hipótesis nula, tendremos evidencia de que la acción sí tiene riesgo sistemático, es decir, que su comportamiento está ligado al del mercado.
Antes de entrar en la regresión, hago un pequeño paréntesis para explicar en qué consiste el modelo CAPM, porque es la base teórica que da sentido a la idea de la beta.
El CAPM es un modelo de valoración muy conocido en finanzas que sirve para calcular la rentabilidad esperada de un activo en función del riesgo que asume. Lo desarrolló William Sharpe (Premio Nobel de Economía en 1990) y su conclusión principal es bastante intuitiva: cuánto mayor es el riesgo, mayor debería ser la rentabilidad esperada.
Como es un modelo teórico, parte de algunas suposiciones que lo simplifican:
El mercado está en equilibrio (oferta y demanda de activos cuadran) y existe competencia perfecta.
Todos los inversores tienen aversión al riesgo y cuentan con la misma información.
Las rentabilidades siguen una distribución normal (es decir, tienen una forma “predecible”).
Solo se tiene en cuenta el riesgo sistemático, el que viene del mercado en general, no el riesgo específico de cada empresa.
A pesar de que estas suposiciones no siempre se cumplen en la realidad, el CAPM se sigue usando muchísimo porque es simple, intuitivo y muy útil para comparar activos.
Su fórmula básica es:
$$
E(r_i) = r_f + \beta ,[E(r_m) - r_f]
$$
Donde:
\(E(r_i)\) → rentabilidad esperada del activo.
\(r_f\) → rentabilidad del activo libre de riesgo (por ejemplo, un bono del Estado).
\(\beta\) → mide cómo se mueve el activo respecto al mercado (su riesgo sistemático).
\(\beta > 1\) → más volátil que el mercado.
\(\beta = 1\) → se mueve igual que el mercado.
\(\beta < 1\) → más defensivo.
\(E(r_m) - r_f\) → prima de riesgo del mercado (lo que “paga” el mercado por encima del activo sin riesgo).
Con esto claro, ya podemos pasar a nuestro modelo de regresión lineal simple. La idea es ver cómo se comporta la acción de Elecnor respecto al mercado:
$$
R^{(E)}_t = \beta_0 + \beta_1 R^{(M)}_t + u_t
$$
Donde:
\(R^{(E)}_t\) → rendimiento de Elecnor en el mes t.
\(R^{(M)}_t\) → rendimiento del mercado (Ibex 35 Total Return) en el mes t.
\(\beta_0\) → intercepto, o alpha (la parte del rendimiento no explicada por el mercado).
\(\beta_1\) → pendiente o beta de la acción (mide su sensibilidad al mercado).
\(u_t\) → todo lo que afecta al rendimiento de la acción pero no viene del mercado.
Para estimar la beta, el alpha y el rendimiento esperado, utilizo rentabilidades mensuales totales (precio + dividendos) de Elecnor y del Ibex 35 Total Return durante los últimos cinco años, es decir, unas 60 observaciones.
Nota. En este primer análisis utilizamos rentabilidades simples y el Ibex 35 (con dividendos) como mercado de referencia, ya que es la referencia natural para un inversor español. En futuros análisis, cuando apliquemos modelos factoriales internacionales (Fama-French), cambiaremos a un índice europeo, lo que seguramente modificará nuestra percepción del riesgo (Beta) y del retorno anormal (Alpha). También emplearemos rentabilidades logarítmicas.
¿Por qué mensuales y no diarias o semanales? Porque es lo que hacen los profesionales, aunque lógicamente esto tiene sus razones:
Los datos diarios tienen mucho ruido: gaps de apertura (el precio de apertura de una sesión es significativamente más alto o más bajo que el precio de cierre de la sesión anterior), días con muy poco volumen, operaciones aisladas… Todo eso distorsiona los movimientos reales y hace que la beta salga artificialmente baja.
Elecnor no es Telefónica ni Santander, y hay días en los que apenas se negocia (lo que se conoce como thin trading). Esto también tiende a reducir la beta estimada.
Eliminan casi toda la autocorrelación de los residuos y los efectos calendario (lunes, fines de mes, festivos, findes…).
Proporcionan regresiones más limpias, con mayores R² y betas más consistentes en el tiempo.
Es literalmente lo que usan Bloomberg, Morningstar, FactSet y el propio CFA cuando enseñan cómo se hace.
¿Cómo se interpretan los coeficientes?
Alpha (\(\beta_0\)). El alpha mide si Elecnor obtiene un rendimiento adicional o inferior al explicado por el mercado.
Si \(\beta_0 > 0\) y es significativo → Elecnor genera “alpha”, es decir, rendimiento extra no explicado por el Ibex.
Si \(\beta_0 = 0\) → cuando el mercado está plano, se espera que Elecnor también lo esté.
Si \(\beta_0 < 0\) → Elecnor suele tener una rentabilidad por debajo del Ibex 35.
Eso sí, siempre hay que recordar que mayor rentabilidad suele implicar mayor riesgo. Por eso, cuando un inversor busca activos con alpha alto, normalmente lo compensan con otra inversión con menos riesgo, es decir, con un alfa más bajo o incluso negativo.
Beta (\(\beta_1\)). La beta es la estrella del modelo. Explica qué porcentaje cambia la rentabilidad de Elecnor cuando el Ibex sube o baja un 1 %.
En finanzas, la beta mide el riesgo sistemático (el riesgo que viene del mercado y que no puedes eliminar aunque diversifiques). Técnicamente se define como la covarianza entre la rentabilidad del activo y la del mercado, dividida por la varianza del mercado. O dicho de otra forma:
$$
correlación × (volatilidad del activo / volatilidad del mercado)
$$
La volatilidad (σ), mide el riesgo total del activo. Es el desvío estándar anualizado de sus rentabilidades. La diferencia entre riesgo total y riesgo sistemático es el riesgo no sistemático, el que sí puede eliminarse diversificando.
Según el Teorema de Gauss-Markov, el modelo debe cumplir cinco supuestos para que los estimadores sean “buenos” (insesgados) y además “los mejores posibles” entre todos los lineales (eficientes). Estos son:
- Linealidad en los parámetros: la relación se puede expresar como una suma de coeficientes multiplicando variables.
- Muestra aleatorio: los datos deben ser representativos, no seleccionados a dedo.
- Media condicional nula: el error no debe estar correlacionado con la variable explicativa (el mercado).
- No autocorrelación del error: un error no debe depender del anterior.
- Varianza del error constante (homocedasticidad): los errores deben tener la misma dispersión en todos los niveles de la variable explicativa.
Si estos supuestos se cumplen, los estimadores se obtienen por Mínimos Cuadrados Ordinarios (MCO) y son MELI: mejor estimador lineal e insesgado.
Una vez descargados los datos y ejecutada la regresión en R, obtenemos el siguiente modelo:

Y esta es la representación gráfica de la regresión:
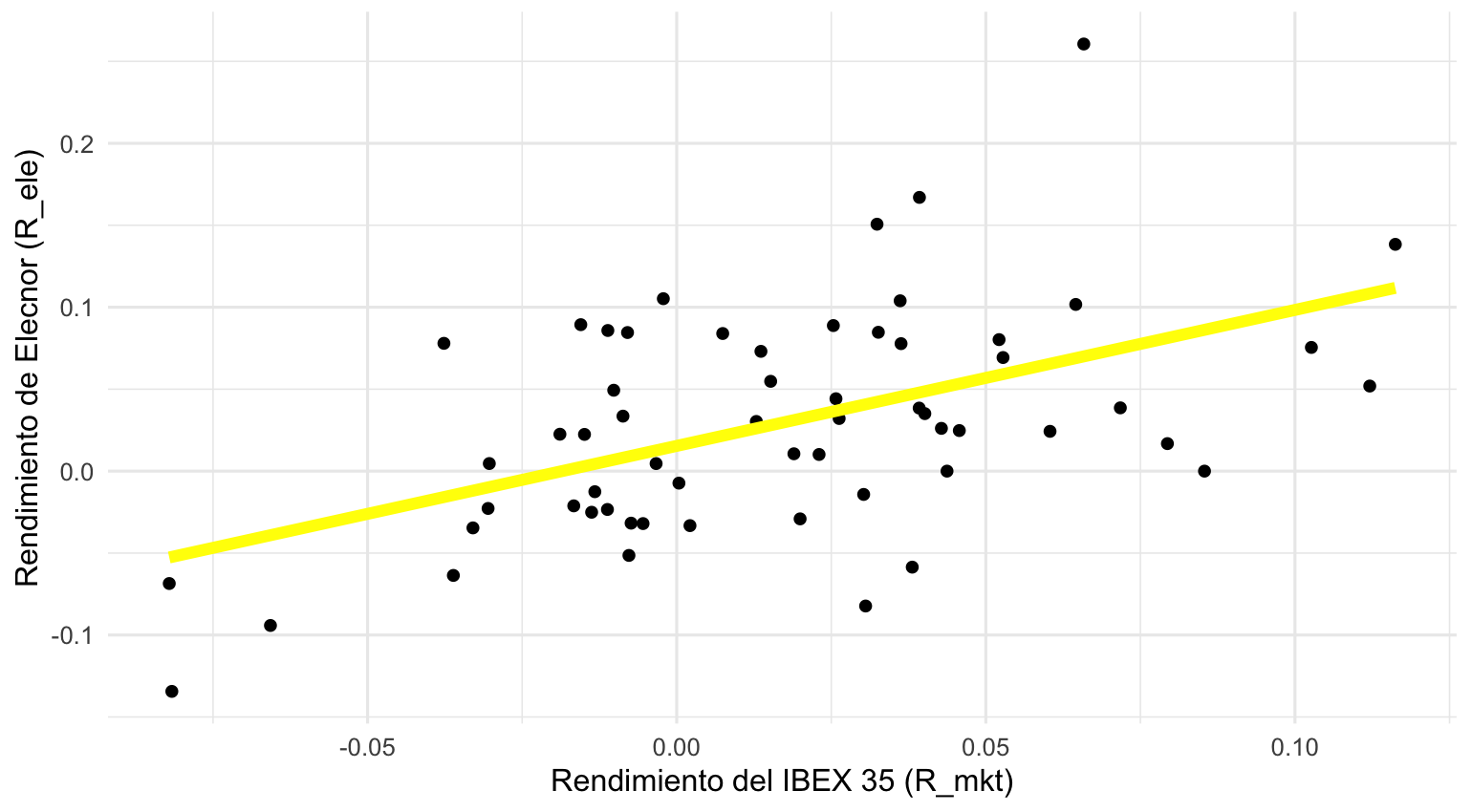
Vamos a interpretar los coeficientes uno a uno.
El intercepto o alpha.
El valor estimado es:
$$
\hat{\beta}_0 = 0.0156
$$
Esto representa la rentabilidad mensual promedio de Elecnor cuando el Ibex no se mueve. En otras palabras, si el mercado permanece plano, Elecnor tendería a generar alrededor de un 1,5% mensual.
Ahora bien, este número viene con matices. Su p-valor es 0,0623, ligeramente por encima del típico 0,05. ¿Qué significa esto?
El alpha no es estadísticamente significativo al 95%. Así que no podemos asegurar que Elecnor genere una rentabilidad adicional independiente del mercado.
Pero su p-valor es de 0,06, lo que nos dice que hay una probabilidad del 94% de que ese rendimiento extra sea real. Por tanto, ¿es posible que Elecnor sí esté generando valor pero nuestro modelo simple no es capaz de captarlo? Esta es la pregunta que resolveremos en los siguientes análisis.
La beta.
El valor estimado es:
$$
\hat{\beta}_1 = 0.8302
$$
Este número explica cómo reacciona Elecnor ante los movimientos del Ibex. Como la beta es menor que 1, Elecnor se comporta como una acción defensiva, es decir:
Cuando el Ibex sube, la acción de Elecnor sube, pero menos. En promedio, un 83% de esa subida.
Cuando el Ibex baja, la acción de Elecnor cae, pero menos. En promedio, un 83% de esa bajada.
Además, la beta es altamente significativa: su p-valor es 2.81e-05, muchísimo menor que 0,05. ¿Esto que quiere decir?
No hay ninguna duda de que Elecnor sí se mueve con el mercado.
El coeficiente es claramente distinto de cero.
Una beta inferior a 1 implica:
Menor volatilidad sistemática que el mercado.
Un comportamiento relativamente estable, típico de compañías de infraestructuras, energía y servicios industriales.
Atractiva para inversores que buscan exposición a renta variable, pero con menor sensibilidad a shocks macroeconómicos.
El coeficiente de determinación (R²).
El valor estimado es:
$$
R² = 0.2629
$$
Esto significa que aproximadamente el 26% de la variación mensual en la rentabilidad de Elecnor se explica por los movimientos del Ibex. ¿Es mucho o poco?
En datos mensuales, donde hay menos ruido, un R² entre el 25 % y 30 % es razonable. Al fin y al cabo, una acción no depende solo del mercado. Peo esto quiere decir que el 74% de lo que hace la acción de Elecnor NO se explica por el mercado. Ese 74% 'misterioso' es lo que intentaremos desgranar en el próximo análisis utilizando modelos multifactoriales.
Test F.
Nos ha salido:
$$
F = 20.68, p < 0.001
$$
Esto significa que el modelo en su conjunto es estadísticamente significativo. Es decir, el rendimiento del mercado es un predictor relevante y útil para explicar el rendimiento de Elecnor.
Hemos confirmado que Elecnor es una acción defensiva (Beta < 1), ideal para protegerse ante caídas. Sin embargo, nos quedamos con la duda del Alpha: el modelo sugiere que bate al mercado, pero no con la suficiente rotundidad estadística.
¿Cambiaría esto si usamos un modelo más avanzado? ¿Y si nos comparamos con Europa en lugar de con España? En la Parte 2, someteremos a Elecnor a un test con el modelo de 4 Factores de Fama-French.
Spoiler: el resultado os sorprenderá.











